January 3, 2022 0

How Does DES Encryption Work in Cryptography?

in Encryption

(17 votes, average: 5.00 out of 5)

Loading...

Until fairly recently, DES was the gold standard in encryption. That’s no longer the case, and today DES and its heir 3DES are known to be insecure and considered obsolete. However, modern encryption still uses similar techniques, so it’s important to understand how DES works. Let’s dig in!

In our last article, we explored the data encryption standard, or DES, in detail. To recap, DES is a symmetric encryption algorithm that uses 56-bit keys (64-bit keys with eight bits reserved for a specific purpose — more on that later) to encrypt data. Despite being used for the protection of sensitive data for decades by the US National Security Agency (NSA), DES has ultimately lost its place in the cryptographic world. However, learning about the inner workings of the DES algorithm can open doors in understanding more recent algorithms like the advanced encryption standard, or AES.

So, it’s time to answer the question, “how does DES encryption work?”

How Does DES Encryption Work? A Look at How DES Works

In a nutshell, DES encryption works by taking a plaintext input and breaking it into smaller chunks (64-bit blocks) to encrypt it using a cryptographic key. Basically, it takes your readable message and, block by block, converts it into unreadable gibberish that can only be decrypted by the decryption key holder.

To better understand how DES encryption works, we first need to understand the fundamental components of this type of algorithm. Then can we get into what part they play in the final algorithm.

An In-Depth Look at the Feistel Structure

The DES algorithm is based on German physicist and cryptographer Horst Feistel’s Lucifer cipher. The Lucifer cipher is based on a combination of transposition and substitution cryptography. It is a block cipher, meaning that it doesn’t encrypt all the data at once, or bit-by-bit like a stream cipher does. Instead, it breaks down the data into blocks which makes the encryption faster and stronger. The size of the block depends on the cipher used, as does the size of the key.

DES is a symmetric cipher. But what does that mean?

• If the same key is used to encrypt and decrypt a block, it is called a symmetric cipher.
• If different keys are used for encryption and decryption, it’s an asymmetric cipher. 

DES uses a 64-bit key to encrypt 64-bit blocks. Of these 64 bits in the key, eight specific bits (known as parity bits) are used to check for errors in the ciphertext. Every eighth bit is used as a parity bit, leaving 56 effective bits in the key. After the verification of the ciphertext, these eight parity bits are dropped. The original key (in normal font) and the parity bits (marked with bold font in the right-most column) are shown in the table below:

1	2	3	4	5	6	7	8
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
25	26	27	28	29	30	31	32
33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
57	58	59	60	61	62	63	64

DES uses initial permutation (IP) and final permutation (FP) functions as part of the Feistel structure. The IP is the first step, which involves rearranging the order of bits in the plaintext input. This is followed by 16 rounds of operations, which then concludes with the final permutation (which is the inverse of the IP).

The order of operations is as shown in the figure below:

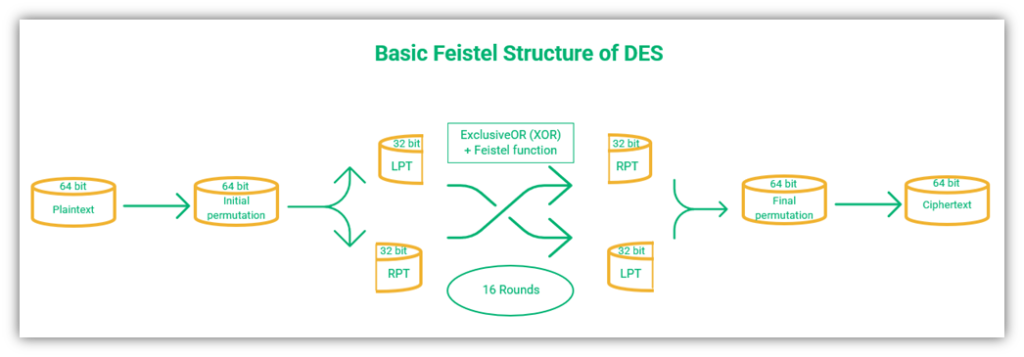
Let’s explore the concepts of initial and final permutation more in more depth.

Initial Permutation (IP)

An initial permutation is carried out just once at the beginning of the encryption process. In DES, after the entire plaintext is divided into blocks of 64 bits each, IP is carried out on each of them. This initial permutation is a step in the transposition process.

The following table shows how the transposition should be carried out on the initial block of 64 bits.

Initial Permutation Table Example:

58	50	42	34	26	18	10	2
60	52	44	36	28	20	12	4
62	54	46	38	30	22	14	6
64	56	48	40	32	24	16	8
57	49	41	33	25	17	9	1
59	51	43	35	27	19	11	3
61	53	45	37	29	21	13	5
63	55	47	39	31	23	15	7

Applying the above table means that the output of the first bit is the input of the 58^th bit, the output of the second bit is the input of the 50^th bit, the input of the last bit is the output of the seventh bit, and so on. An extra layer of security is added to the Feistel structure by scrambling the input.

DES Encryption Relies on the Feistel Function

Test words go here to see how it affects the layout. In our previous article on DES encryption, we mentioned that it’s important to learn about DES, even though it is obsolete, because many other encryption algorithms like Twofish, Blowfish, and GOST are based on the Feistel function. This function is also known as Luby-Rackoff block cipher or Feistel network.

The Feistel function is a round function, meaning that rounds of encryption operations are carried out a specified number of times. Before each round, the data is divided into two parts – the left plain text (LPT) and the right plain text (RPT).

In DES, a total of 16 rounds of Feistel’s function occur, comprising the following steps:

1. The output of the IP is taken as an input for the Feistel function, let’s call it X. The size of X is 64 bits.
2. X is divided into two parts with 32 bits each – the LPT and RPT.
3. Subkeys (K_1, K₂, K_n, etc.) are derived from the original key, and one key is applied during each round.
4. The result (f) of LPT is carried out using RPT and K₂ – f(RPT,K₁).
5. Mathematical function XOR (explained below) is performed on f(RPT,K₁) and LPT, resulting in L₁.
6. L₁ is swapped with RPT. So, the next function is performed on RPT, resulting in L₂.

ExclusiveOR (XOR) Function

The XOR function (pronounced “ex-or”), is a logical operator that compares two sets bit by bit. It’s a Boolean function, which means it returns a true or false value (0 or 1). If the bits match, XOR returns the value 0, and if they don’t match, XOR returns 1. XOR is represented by the symbol Ꚛ. The function is represented by L₁ = f(RPT,K₁) Ꚛ LPT.

Set 1	Set 2	Output
0	0	0
0	1	1
1	0	1
1	1	0

As shown in the above table, if the inputs from the two sets match, the resulting output is 0. Otherwise, if they do not match, the output is 1. Here’s an example of the XOR function:

1011010100 Ꚛ 0010111011

The resulting output will be 1001101111.

The purpose of applying the XOR function is to make brute force attacks more difficult by ensuring that decryption of the text is not possible without the XOR key. 

The following figure shows how the Feistel function in DES works:

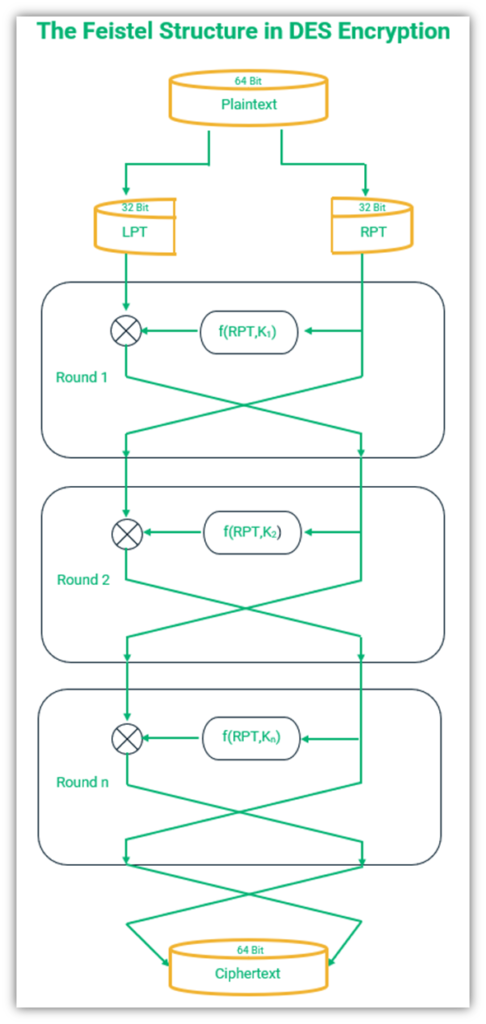
The above figure shows the steps followed during the encryption of the plaintext. It is noteworthy that the left and the right text are swapped one last time after the 16 rounds are completed. If this step is missed for any reason, the decryption of the text will not be possible.

Final Permutation (FP)

Now that we understand how the initial permutation works, it’s time to break down the final permutation. The final permutation table is the inverse of the IP. So, the final step of the encryption is done by doing the exact opposite of the first step.

The final permutation table is as follows:

40	8	48	16	56	24	64	32
39	7	47	15	55	23	63	31
38	6	46	14	54	22	62	30
37	5	45	13	53	21	61	29
36	4	44	12	52	20	60	28
35	3	43	11	51	19	59	27
34	2	42	10	50	18	58	26
33	1	41	9	49	17	57	25

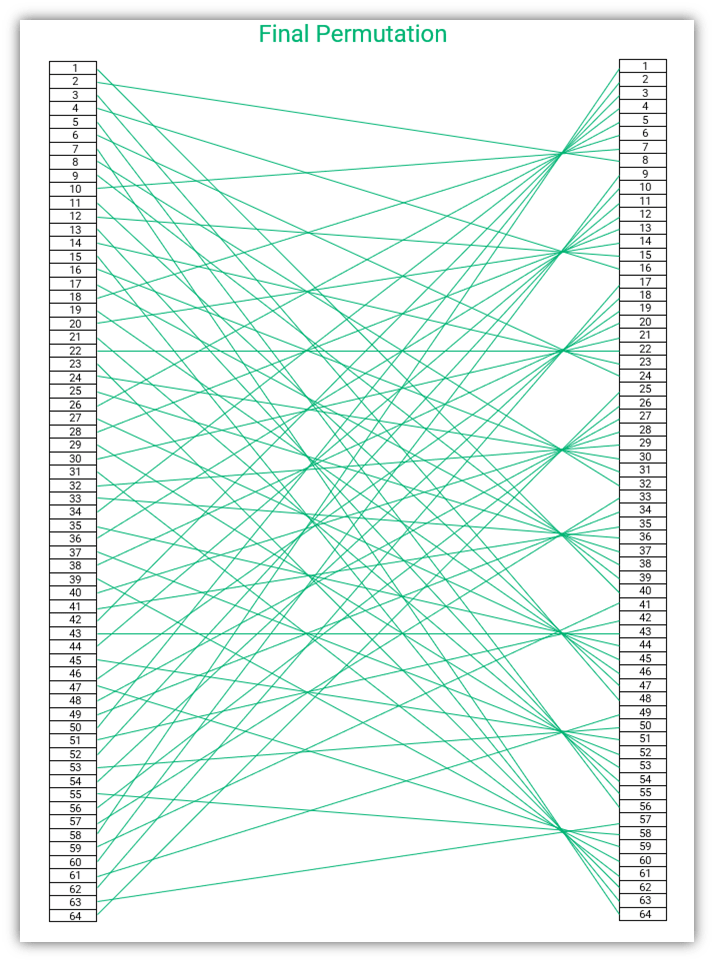
In the final permutation, the inverse of IP is used. Do you remember we had the output of the first bit as the input of the 58^th bit in IP? In FP, we invert that — meaning, the input of the 58^th bit is the output of the first bit. You can see that the 58^th bit is ‘1’ in the FP table (marked in bold font in the table for your reference, second column from the left in the bottom row). The input of the seventh bit is the output of the 64^th bit (the last bit).

The initial permutation table is not a matrix but a vector. Therefore, you will see that when we connect the input and the output, as shown in the figures IP and FP given above, we will be able to see the inverse pattern. However, the tables will not be reversed exactly. Vectors and matrices are complex mathematical concepts, and although I would like to go into more detail, I’m putting on my brakes to keep this article from turning into a book!

A Quick Look at DES Decryption and How It Works

DES encryption, like other encryption algorithms, is a two-way process. This means that information is encrypted with the intention of it being decrypted by the appropriate party. (Otherwise, if the right person can’t read it, what’s the point in encrypting and sending the data at all?)

We saw that the DES algorithm uses IP and the Feistel function for encryption. To decrypt DES-encrypted data, in a general sense, the same steps are followed but in basically reverse order. Instead of the plaintext input, the 64-bit ciphertext output is used at the beginning of the process, and subkeys are used to help reverse engineer the data to calculate the original input plaintext.

The 64-bit ciphertext is divided into two 32-bit blocks. After that, the same keys that were utilized to encipher the plaintext are used to decrypt the ciphertext. The main difference in the process is the generation of keys – during encryption, the keys are generated, whereas during decryption, the keys generated earlier for encryption are used in reverse order. The encryption key K₁ becomes the decryption key K_16, and K₂ becomes K₁₅. Other than that, all the steps are carried out in the same way as with encryption.

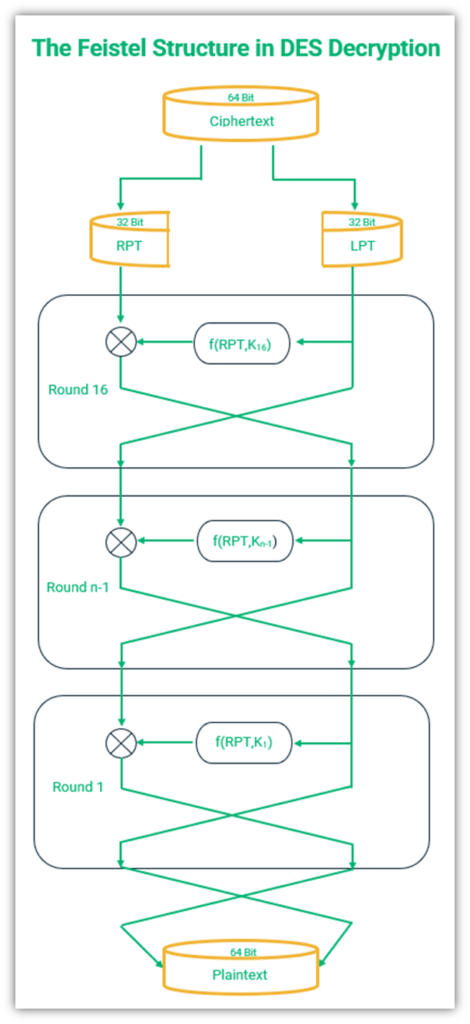
A detailed figure showing how Feistel structure works in DES decryption

Final Thoughts on How DES Encryption Works

DES is a complex algorithm that works by dividing an input text into smaller 64-bit blocks. Each block then goes through an initial permutation, and the result of the initial permutation is further divided into two parts called LPT and RPT. These two parts then go through the Feistel function for 16 rounds. After these rounds, the text goes through the final permutation. The resulting text is the ciphertext. The process is essentially reversed at the time of decryption.

This DES algorithm serves as a base for many encryption algorithms used at present. Modern algorithms like AES and Twofish are more complex and so more difficult to crack. Most trustworthy SSL/TLS certificates use AES encryption to secure data transferred online and we’ll investigate AES in an upcoming article.

• #Data Encryption Standard
• #DES
• #How DES Works